Expanding Spherical Wavefronts are standard physics:

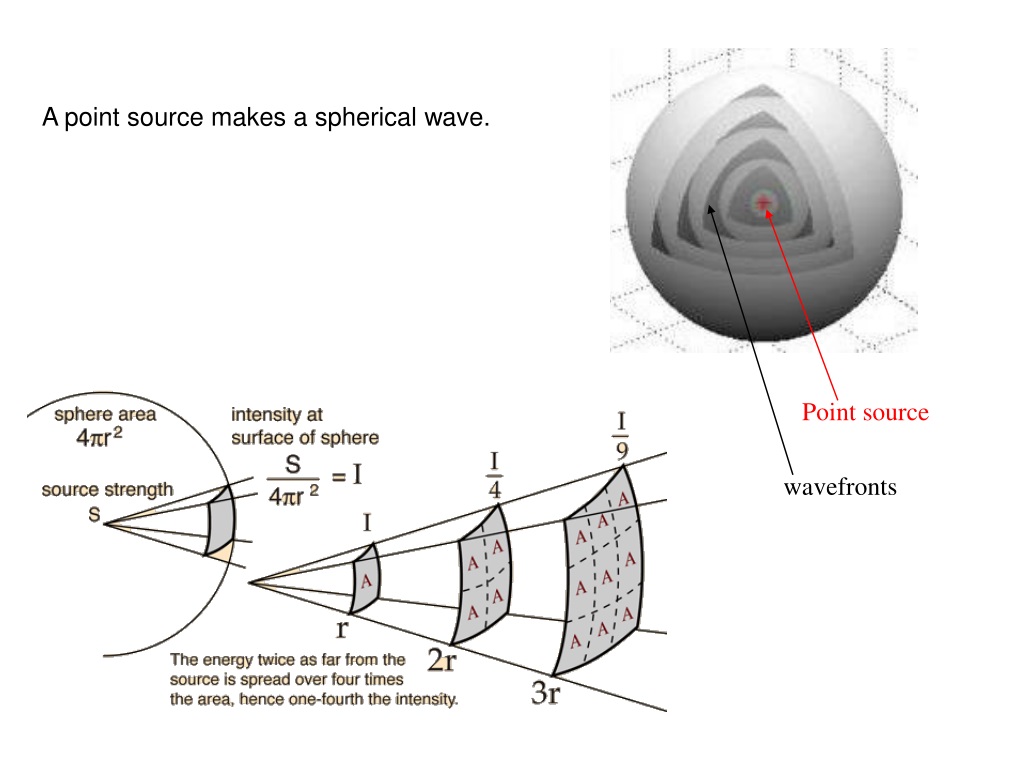
Credit: Gong Gu, https://fr.slideserve.com/oster/ece341-electromagnetic-fields-powerpoint-ppt-presentation

The Expanding Spherical Wavefronts depicted above are physical entities. They illustrate the behavior of light as emitted omnidirectionally by a “point source” emitter. Point source, as always in physics, is a mathematical term of art, there being no physical meaning to the mathematical concept of a dimensionless “point”. A source can be treated mathematically as point-like, however, for an observer distant enough that the emitting source’s dimensions are small relative to the radial distance to the observer.

In the foregoing sense, a typical galaxy can be treated as a point source at large ( >100 million lightyears) distance. The nested shells of the model can be considered as representing either successive positions of a single wavefront over time or an instantaneous representation of continuously emitted successive wavefronts from a typical, omnidirectional emitter such as a galaxy.

This nested shell model can also be invoked to illustrate a ubiquitous inverse electromagnetic phenomenon. Replacing the emitter with an observer, the nested shells can be seen as representing notional spheres existing at various, arbitrary radial distances from the observer. At any given radial distance of cosmological significance from the observer the notional shell will have on it some number of galaxies. Such a notional shell also defines a notional volume which must also contain some number of galaxies. This geometrical situation is only relevant to the observer; it is not, as in the ESW case, a physical entity.

Elaborating a bit, we can define a cosmological radial unit of r = 100 million lightyears. That radial unit then defines a sphere with a surface area proportional to r² and a volume proportional to r³, For illustrative purposes we make a simplifying (and unrealistically low) assumption that any r³ unit volume contains on average 1000 galaxies.

Observers whose observational range extends out 1 radial unit will observe their “universe” to contain 1000 galaxies. If those same observers improve their technology so that their range of observation extends to 2 radial units they will find themselves in a “universe” that contains 8000 galaxies. If their range doubles again to 4r their “universe” will now contain 64,000 galaxies.

Every time the observational range doubles the total number of galaxies contained in the newly expanded “universe” will increase by a factor of 8 or 2³. Of that 8-fold increase 7/8 of the total number of galaxies will lie in the newly observable portion of the total volume. This all follows from straightforward geometrical considerations.

Now let us return to the shell model centered on an omnidirectional emitter. The same geometric considerations apply here but this time with respect to an Expanding Spherical Wavefront. At 1r a wavefront will have encountered 1000 galaxies, at 4r, 64,000 galaxies and at 8r it will have encountered a total of 512,000 galaxies. As mentioned earlier, these numbers may be unrepresentative of the actual number of galaxies encountered, which could be considerably higher.

When an ESW encounters a galaxy some portion of that wavefront is absorbed by the galaxy representing a loss of energy by the wavefront and a corresponding gain of energy by the galaxy. This leads to two further considerations, the first related to direct observations. An ESW will lose energy as it expands in proportion to its volumetric expansion assuming a constant average galactic density . The energy loss will be be insignificant for each individual galactic encounter but the aggregate loss will increase exponentially at large radial distances. An increasing loss of energy with distance is an observed fact (cosmological redshift) for the light from galaxies at large (>100Mly) cosmological distances.

The second consideration is that in some finite time period relative to the emitter all of an ESW’s energy will be absorbed by intervening galaxies (and any other non-luminous baryonic matter). The cosmological range of an ESW is inherently limited – by standard physical considerations. In a sense, their is a notional cosmic wall, relative to the emitter, beyond which its ESWs cannot penetrate.

Reverting once again to the observer’s point of view, it follows that the observers cannot receive electromagnetic signals from sources that have reached the limits of their range – the cosmic wall discussed in the previous paragraph. It also follows directly that the observer is surrounded by a notional cosmic wall, relative only to the observer, beyond which more distant emitters cannot be observed. This wall has no physical significance except from the observer’s local Point-Of-View – it is the aggregate of all the ESW notional walls that surround the observer.

That notional wall is real however in the sense that it defines the limits of any observer’s observational range, just as the wall encountered by an ESW limits the range of its expansion. In both cases we are dealing with a relativistic POV. The ESW just before it reaches its wall encompasses an enormous cosmological volume relative to its source emitter’s location. Observers, just before encountering their notional wall, observe an enormous cosmological volume relative to their three dimensional locale.

Keeping in mind the earlier discussion of the spherical geometry of ESWs, it is interesting to consider that immediately in front of an observer’s notional wall there lies a vast volume of some nominal thickness containing galactic emitters that are still observable. The number of those emitters has increased as R³, while their cosmological redshift has increased as R³, where R is the observer’s radial distance from the remote sources. Beyond that radial distance lies the notional wall at which all observations cease. In that context the observer’s wall can be thought of as a concave, spherical shell against which all foreground observations are projected. Because of the geometrical considerations mentioned, we should expect the most distant visible galaxies to cover the notional, concave, spherical surface of the observer’s cosmological view.

What we arrive at then is a picture much like that proposed by Olber’s Paradox, the only difference being that Olber did not account for the energy loss of light so he expected that the night sky should be uniformly bright in the visible spectrum. What we observe, of course, is a night sky uniformly bright in the microwave spectrum.

The existence of the Cosmic Microwave Background is consistent with the galaxy distribution and energy loss to be expected by using the Expanding Spherical Wavefront framework of standard physics to model the Cosmos we observe. The only assumptions necessary to achieve this result are of an average galactic density on cosmological scales and that the field of galaxies extends sufficiently far for the geometrical arguments to hold.