An earlier post on Expanding Spherical Wavefronts made a qualitative argument that an ESW should sustain an energy loss as it expands through the Cosmos. In a more recent post it was argued that gravitational effects are a consequence of matter/electromagnetic-radiation interactions. As a follow-up, this post offers a quantitative demonstration that standard gravitational-redshift-based-math can be applied to an ESW to generate a cosmological redshift correlated with distance:
Terms & Definitions:
z = ((1-(rs/Resw))^(-1/2))-1
rs = Schwarzschild radius = 2GM/c2
Res = successive radii for an Expanding Spherical Wavefront in lightyears
Resw = successive radii for an ESW in meters
M = Calculated mass for a sphere at selected radii, assuming an average cosmological density of 1E-26 kg/m3. The average density is a free parameter in the model but the results are highly sensitive to this particular value. A variation of +/- 10% produces outcomes that seem unrealistic.
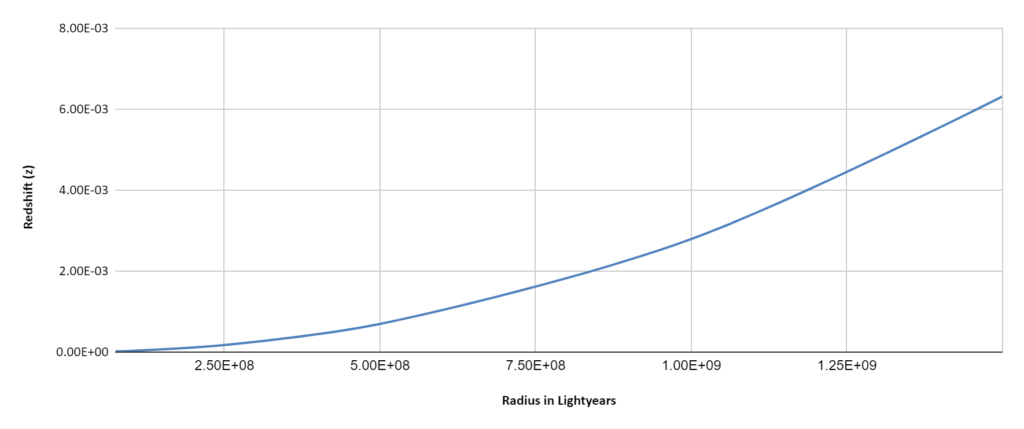
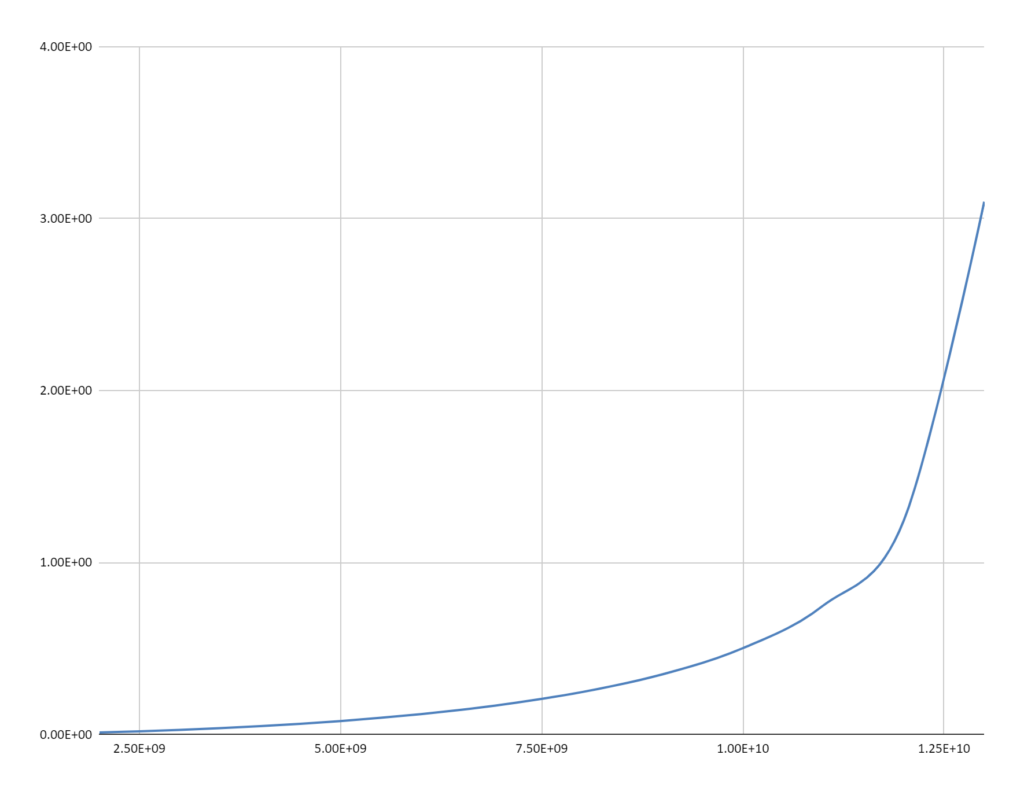
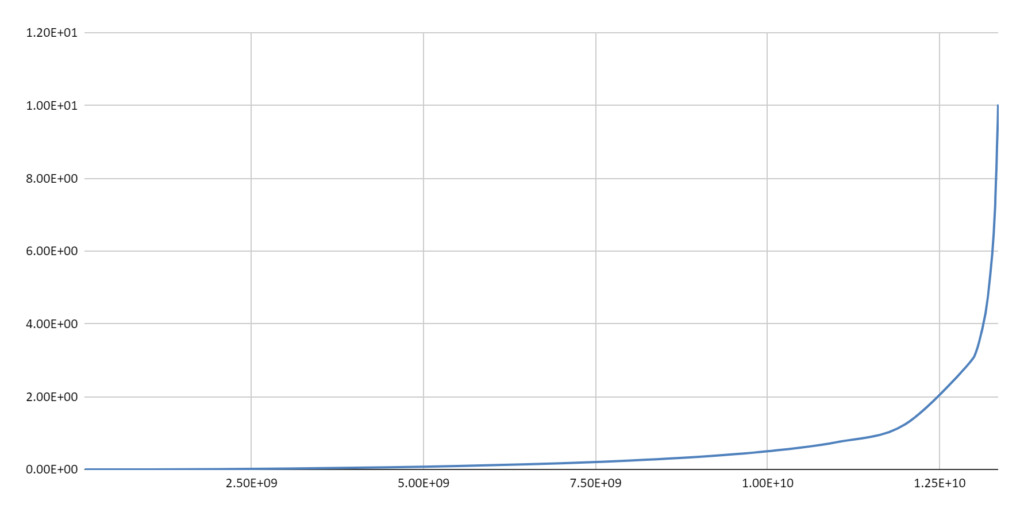
All in all, this is nothing more than a proof of concept – but it is an intriguing one. Two pieces of standard physics can be put together to produce a cosmological redshift-distance relation that is similar to the one presented by the standard model. The three graphs of redshift-distance are taken from the table and illustrate scale differences over the range of the table. A short discussion follows the 3rd graph.
| Res (Ly) | Resw (meters) | rs | M (kg) | z | |
| 1 | 7.50E+07 | 7.08E+23 | 2.22E+19 | 1.48E+46 | 1.57E-05 |
| 2 | 1.00E+08 | 9.44E+23 | 5.25E+19 | 3.52E+46 | 2.78E-05 |
| 3 | 2.50E+08 | 2.36E+24 | 8.20E+20 | 5.50E+47 | 1.74E-04 |
| 4 | 5.00E+08 | 4.72E+24 | 6.56E+21 | 4.40E+48 | 6.96E-04 |
| 5 | 1.00E+09 | 9.44E+24 | 5.25E+22 | 3.52E+49 | 2.79E-03 |
| 6 | 1.50E+09 | 1.42E+25 | 1.77E+23 | 1.19E+50 | 6.32E-03 |
| 7 | 2.00E+09 | 1.89E+25 | 4.20E+23 | 2.82E+50 | 1.13E-02 |
| 8 | 2.50E+09 | 2.36E+25 | 8.20E+23 | 5.50E+50 | 1.79E-02 |
| 9 | 3.00E+09 | 2.83E+25 | 1.42E+24 | 9.50E+50 | 2.60E-02 |
| 10 | 3.50E+09 | 3.30E+25 | 2.25E+24 | 1.51E+51 | 3.59E-02 |
| 11 | 4.00E+09 | 3.77E+25 | 3.36E+24 | 2.25E+51 | 4.77E-02 |
| 12 | 4.50E+09 | 4.25E+25 | 4.78E+24 | 3.21E+51 | 6.16E-02 |
| 13 | 5.00E+09 | 4.72E+25 | 6.56E+24 | 4.40E+51 | 7.78E-02 |
| 14 | 5.50E+09 | 5.19E+25 | 8.74E+24 | 5.85E+51 | 9.65E-02 |
| 15 | 6.00E+09 | 5.66E+25 | 1.13E+25 | 7.60E+51 | 1.18E-01 |
| 16 | 6.50E+09 | 6.13E+25 | 1.44E+25 | 9.66E+51 | 1.43E-01 |
| 17 | 7.00E+09 | 6.61E+25 | 1.80E+25 | 1.21E+52 | 1.73E-01 |
| 18 | 8.00E+09 | 7.55E+25 | 2.69E+25 | 1.80E+52 | 2.46E-01 |
| 19 | 9.00E+09 | 8.49E+25 | 3.83E+25 | 2.57E+52 | 3.49E-01 |
| 20 | 1.00E+10 | 9.44E+25 | 5.25E+25 | 3.52E+52 | 5.02E-01 |
| 21 | 1.10E+10 | 1.04E+26 | 6.99E+25 | 4.68E+52 | 7.50E-01 |
| 22 | 1.20E+10 | 1.13E+26 | 9.07E+25 | 6.08E+52 | 1.24E+00 |
| 23 | 1.30E+10 | 1.23E+26 | 1.15E+26 | 7.73E+52 | 3.10E+00 |
| 24 | 1.31E+10 | 1.24E+26 | 1.18E+26 | 7.91E+52 | 3.71E+00 |
| 25 | 1.32E+10 | 1.25E+26 | 1.21E+26 | 8.09E+52 | 4.74E+00 |
| 26 | 1.33E+10 | 1.25E+26 | 1.24E+26 | 8.28E+52 | 7.00E+00 |
| 27 | 13,350,000,000 | 1.26E+26 | 1.25E+26 | 8.37E+52 | 1.00E+01 |
| 28 | 13,400,000,000 | 1.26E+26 | 1.26E+26 | 8.47E+52 | 3.49E+01 |
| 29 | 13,405,000,000 | 1.26E+26 | 1.26E+26 | 8.48E+52 | 1.75E+02 |
| 30 | 13,405,100,000 | 1.26E+26 | 1.26E+26 | 8.48E+52 | 2.39E+02 |
| 31 | 13,405,200,000 | 1.26E+26 | 1.26E+26 | 8.48E+52 | 6.48E+02 |
Discussion
There are several interesting aspects to these results. The initial radius of 75M lightyears is arbitrary and lies just inside the 100Mly radius that can be considered to encompass the “local” Cosmos. The final radius in the model goes asymptotic at the range imposed by the math.
What is happening in the math is the Schwarzschild radius (rs) is catching up with the Expanding Spherical Wavefront being modeled. This is because the rs is increasing in proportion to the enclosed mass which is increasing as Resw3 while the ESW itself is only increasing as Resw2. This is the inverse of what happens (according to the Schwarzschild solution to GR) in the case of a mass undergoing gravitational collapse. In that situation the collapsing body converges inward toward the rs as the mass remains constant.
It should be noted that the rs is an artefact of the model; it is a coordinate singularity and not physically significant. This indicates that the model has broken down at that point by virtue of having produced a division by zero result. It can be argued that this is a consequence of the model not taking into account the variation in the speed of light in a gravitational gradient.
It is also striking that the redshift of the ESW model goes asymptotic at approximately the same cosmological distance (13.4Gly) that the standard model redshift does (13.8Gly). The difference is that in the ESW model the redshift is a consequence of the energy loss to the expanding spherical wavefront attributable to its gradual absorption by intervening galaxies. In the standard model the energy loss is a consequence of a model-inferred but unobservable “universal expansion” – which leaves the lost energy physically unaccounted for.
One other point of note, in the ESW account of redshift the cosmological conditions at the source of the redshifted light are assumed to be approximately the same as they are in our “local Cosmos”. In the standard model, of course, the cosmological conditions at the largest implied redshift distances are thought to be significantly different due to the nature of the evolving “expanding Universe” that the model assumes. The recent JWST observations contradict the standard model’s picture of an evolving “Universe”.

Really interesting.
Pingback: Island Universe Cosmology v4.0 | This Island Universe